Curve Primitives
- A CurvePrimitive is a bounded continuous curve.
- All curves implement methods (e.g.
fractionToPointto refer to "fraction" position along the curve.fraction=0is the startof the primitivefraction=1is the end of the primitive- increasing fractions always move forward along the primitive.
- curves implment their equations with the fraction representing the parameter in their most natural equations.
- All curves also support methods to deal with true distance along the curve. These include
curve.curveLengthBetweenFractions (startFraction, endFraction)curve.moveByDistanceFromFracton (startFracton, distance)- Fraction position along the curve is strictly proportional to true distance along the curve only for a limited number of curve types:
- LineSegment3d
- Arc3d
- TransitionSpiral
- Other curve types that have more complicated (non-proportional) fraction-to-distance relations are
- elliptic arcs
- bspline curves
- linestrings
- When movement "by distance" along a chain of curves (of varying types) is required, the
CurveChainWithDistanceIndexwill act like a single curve (starting and ending at fractions 0 and 1), with the fraction mapped to true distance along the chain.
lineSegment
- A line segment is a portion of an infinite line.
- Json Fragment:
[{"lineSegment":[[0,0,0], [3,0,0]]} typescript object:
const myLineSegment = LineSegment.create (Point3d.create (1,2,3), Point3d.create(6,4,2));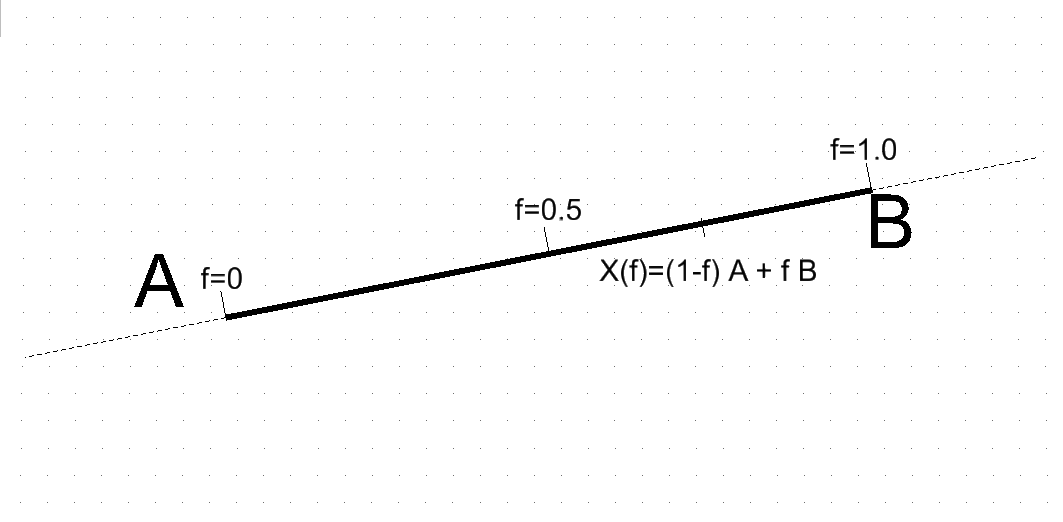
- Fractional Parameterization:
A = start point B = end point f = fraction varying from 0 to 1 Point X(f) at fractional position f along the lineSegment is X(f) = (1-f) * A + f * B
- Fractional Parameterization:
lineString
- A LineString is an array of points that are to be connected by straight lines.
- Json Fragment:
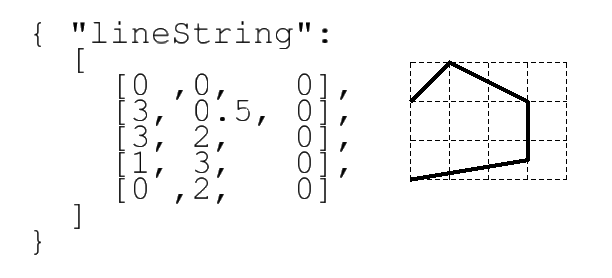
- Typescript object:
const myLineString = LineString.create ([point0, point1, point2 ....]); - Fractional Parameterization
Having both individual line segments and the composite linestring complicates parameterization.
- As with all CurvePrimitives, the fractional parameterization for the complete linestring must have
fraction=0at the start andfraction=1at the end. - The fractional positions of each inerior vertex are then defined at equal intervals in the fraction space.
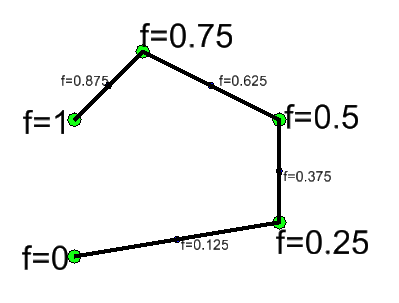
- Hence in the example, with 4 segments the vertex fractions increment by one quarter.
- Within each segment, the fraction interval is mapped as if it were a line segment.
- Note that having uniform vertex-to-vertex fraction means that the distance-along-the-linestring is not proportional to fraction-along-entire-linestring. Fraction and distance changes are only proportional within individual segments.
arcs (circular and elliptic)
An arc primitive is a portion of a circular or ellipticla arc. The equations for a complete elliptic arc require a center point and two vectors. The start and end of a partial arc are controlled by two angles.
The equational forms for circular and elliptic cases are identical. Telling whether a given arc is true circular requires examination of the vector coordinates.
The stroking equation that maps an angle to a coordinates to points around a (full) elliptic (or circular) arc is
C = center point
U = vector from center point to 0-degere point
V = vector from center point to 90-degree point.
theta = angle
X(theta) = C + cos (theta * U + sin(theta) * VTrue Circles
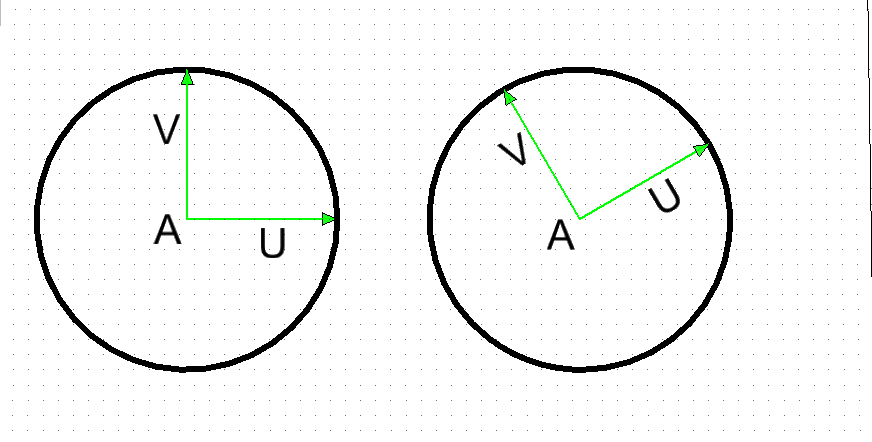
- If the
UandVvectors are (both) perpendicular and the same length, this is a true circle. - In the both circles below, the
UandVare identical length and perpendicular to each other. - For the left circle,
UandVhappen to be in the global x and y directions. - For the right circle,
UandVare still identical length and perpendicular, but are both rotated away from global x and y. This still traces a circle, but the "0 degree" point is moved around the circle. - When the circular arc conditions are true, the angle used in the equations is an the actual physical angle between the
Uvector and the vector from the center toX(theta).
Ellipse
If the U and V vectors either (a) have different lengths or (b) are not perpendicular, the ellispe is non-circular.
If U and V are perpendicular, their lengths correspond to the common usage of "major" and "minor" axis lengths. But the perpendicular condition is not required -- non-perpendicular vectors occur due to transformation and construction history.
Angular limits
To draw an arc that is not the complete circle or ellipse, simply limit the theta range to something other than 0 to 360 degrees.
theta0 = angular start point
theta1 = angular and point
f = fraction varying from 0 to 1
theta(f) = (1-f) * theta0 + f * theta1
Point X(f) at fractional position f along the arc is
X(f) = C + cos (theta(f)) * U + sin(theta(f)) * V- Angles theta0 and theta1 can be negative and can be outside of 360 degrees.
- Anlge theta1 can be less than theta0
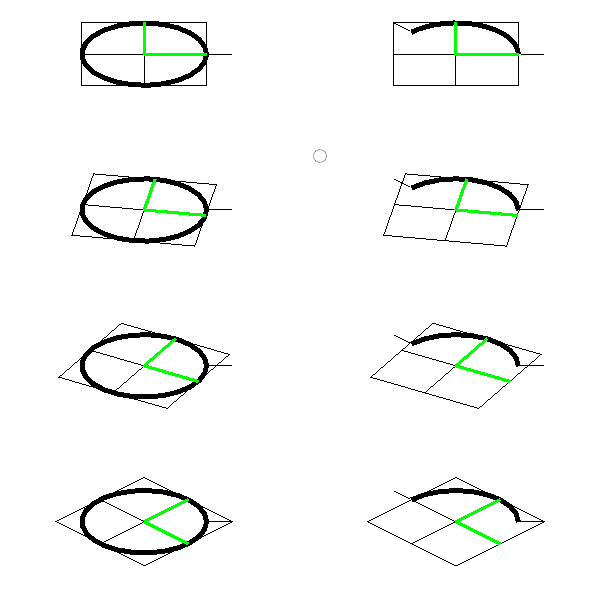
Examples of arc sweep
| start and end angles | CCW signed sweep angle | image |
|----|----|---|
| (0 to 360) | 360 | 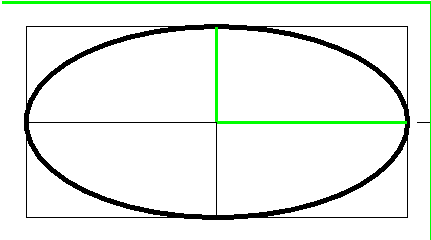 |
| (0 to 135) | 135 |
|
| (0 to 135) | 135 | 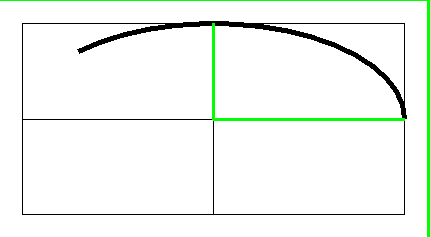 |
| (270 to 495) | 225 |
|
| (270 to 495) | 225 | 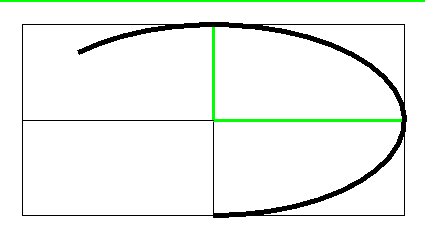 |
| (90 to 270) | 180 |
|
| (90 to 270) | 180 | 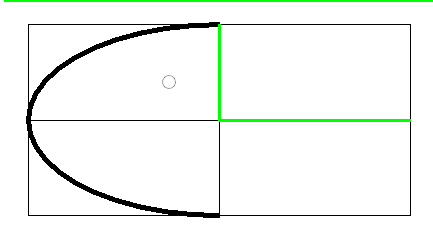 |
| (90 to 405) | 315 |
|
| (90 to 405) | 315 |  |
|
Examples with json fragments

bspline curves
A BSplineCurve3d (or BSplineCurve3dH) is a curve that (loosely) follows a sequence of control points.
Internally, the curve is a is a sequence of polynomial curves that join together smoothly. Call each of those separate pieces a span.
The "control point" structure has remarkable properties for computation:
- The curve never leaves the overall xyz range of the control points.
- This bounding propery applies "from any veiwpoint", not just in the coordinate system where they are given.
- Even tighter, the curve is contained within the convex hull of the control points.
- No plane can intersect the curve more often than it intersects the control polygon.
- that is, the polygon may overestimate the number of intersections, (i.e. suggest false intersections), but it never underestimates.
- Inspection of the control polygon gives similar "never understimate" statements can be made about other propperties such as
- the number of inflections.
- the number of minima and maxima of the curve and its derivatives.
- The use of "weights" on the control points allows a bspline curve to exactly trace circular and elliptic arcs without use of trig functions.
References
There are innumerable books and web pages explaining splines. There is a high level of consistency of the concepts -- control points, basis functions, knots, and order. But be very careful about subtle deatils of indexing. Correct presentations may superficially appear to differ depending on whether the writer has consdiders n indices to run
- C-style,
0 <= i < n(with indexnnot part of the sequence) - Fortran style ,
1<=i<n - (rare)
0<=i<=n
Some typcial descriptions are:
- https://en.wikipedia.org/wiki/B-spline
- http://web.mit.edu/hyperbook/Patrikalakis-Maekawa-Cho/node17.html
- https://www.cs.unc.edu/~dm/UNC/COMP258/LECTURES/B-spline.pdf
Be especially careful about the number of knot counts, which can differ by 2 as described in the "overclamping" section.
The order of the bspline is the number of control points that are "in effect" over an individual span.
- The first span is controlled by the first
ordercontrol points, i.e. those indexed0, 1, .. (order-1). - The next span is controled by control points indexed
1,2,..order.- That is, there is a "moving window" of
orderpoints that control successive spans. - When moving from one cluster of
ordercontrol points to the next, the first (left) point of the first cluster is dropped and a new one is added at the right.
- That is, there is a "moving window" of
- The sharing of control points provide the critical properties for the curve:
- No matter how many control points there are (think dozens to hundreds), each individual span is controled by only
orderpoints. - this "local control" prevents changes "far away" in the control points from causing unexpected global changes in the curve.
- The sharing of
order-1points works into the formulas to guarantee smoothness of the curve. - Specifically, for a bspline of given
order:- If the knots are strictly increasing (no duplicates) the curve has
order-2(i.e.degree-1) continuous derivatives. - Introducing repeated knots reduces the continuity. In particular, with
order-1repeated knots there is a cusp (abrupt slope change) at that knot.
- If the knots are strictly increasing (no duplicates) the curve has
- No matter how many control points there are (think dozens to hundreds), each individual span is controled by only
Summary
The required data for a bspline curve is:
|-----|-----|------|
| name | type | remarks |
| control points | array of N points |
| order | number | the most common orders are 2 through 4; higher order gives smoother curves, but with performance cost. |
| | | Order higher than 10 is discouraged |
| | | 3 (quaratic curve, degree 2)
| | |or 4 (cubic curve, degree 3) |
| knots | array of (N + order - 2) numbers | See knot paragraph |
order
- The
orderis the number of control points that affect each span of the curve. - Bspline equations hypothetically allow any integer
order. - For practical use the common orders are quite low - 2,3,4, with occasional 5 through 8
order=2- the Bspline is a collection of straight lines (degree 1)order=3- the Bspline is a collection of quadratic curves. (degree = 2) (Quadratic curves with weights can exactly trace circular and elliptic arcs)order=4- the Bspline is a collection of cubic spans. These can have inflections within a span.- many graphics systems focus on cubic (
order=4, degree=3bsplines. These are a good balance of curve flexibility and computational cost.
- Conversationally, if one is thinking of "quadratic" cubic "curves", it is common to refer to the
degree, which is one less than the order- the
degreeis the highest power appearing in the polynomial - A conventional polynomial form would have coefficients of terms with power 1,2, through
degree. - That polynomial would alwo include a constant term that does not muliply a power of x.
- Hence there is one more coefficient than the degree.
- textbook algebra discussions prefer reference to the highest power (
degree) because that is short indicator of complexity - Bspline discussion prefers reference to
orderrather thandegreebecause all of the internal matrix manipulations must account for that many coefficients.
- the
knots
- The knots are an array of sorted numbers.
- If there are K knots:
- Each cluster of
2*order-2knots (i.e.2*degreeknots affects a single span - The knots index at
knots[i]throughknots[i+2*order-3](inclusive) affect spani. - That knot values for that span are from
knots[i+order-2]throughknots[i+2*order-2].
- Each cluster of
- Within the knots sequence, the values must never go down.
Clamping
- If knot values are strictly increasing -- e.g. 1,2,3,4,5, -- all the way to the end, the curve does not pass through the first and last control points.
- Having the right number of identical knot values "at the ends" makes the curve (a) pass through the end control points and (b) have tangent direction towards the immeidate neighbor.
- Specifically, for a curve of given
degree, exactly that number of repeated knots creates the usual "clamped" effects.- For instance, for a cubic curve, the knots
[0,0,0,0.25,0.5,0.75,1.1.1]will- Pass through both end points, with tangent along the end segment of the polygon
- have interior knot breaks at 0.25, 0.5 and 0.75.
- For instance, for a cubic curve, the knots
OVERCLAMPING
- An important point for exchanging knots with legacy graphics systems (including Microstation and Parsolid) is that there is a long-established (an unneccessary) practice of having one extra (unused) knot at each end.
- That is, the overclamped cubic knot sequence with breaks at 0.25, 0.5, and 0.75 would be
[0,0,0,0,0.25,0.5,0.75,1.1.1,1]. - The equations for the bsplne will never reference the extra knots at the beginning and end.
- In the overclamping convention, the relation of counts of control points (N) and (overclampled) knots is
...
...numberOfKnotsWithOverclamping = N + order = numberOfControlPoints + order
In imodeljs
- the spline classes (
BsplineCurve3d,BSplineCurve3dHand surface partners) internally do not overclamp. - The API for constructing splines accepts both styles of input. The order, knot count, and control point counts distinguish which style is being used.
- If
numberOfControlPoints === numberOfKnots + orderthe curve is overclamped, so the first and last knot values are not saved in the bspline curve object - If
numberOfControlPoints === numberOfKnots + order - 2the knots are all used.
- If
- The curve objects have method
...
curve.copyKnots(includeExtraEndKnot: boolean)
...
to extract knots. The caller can indicate if they prefer overlcamped knots by passing
truefor theincludeExtraEndKnotparameter. - When knots are written in
iModelJsonobjects, they are written with overclamp.
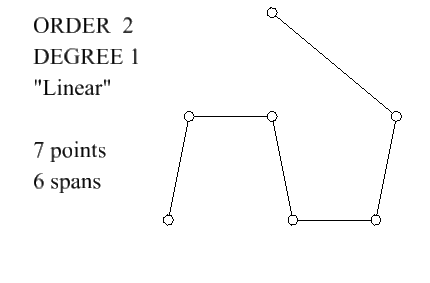
Example: Order 2 (linear) bspline curve
- An order 2 bspline curve has degree 1, i.e. is straight lines
- The circles in the figure for order 2 bspline are both control points and span breaks.
- This is the only order for which the span breaks occur at the control points.
- The direction (first derivative) changes at control point
- Hence there are sharp corners exactly at the control points.
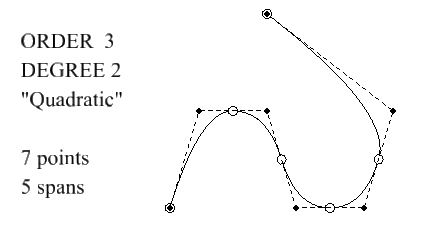
Example: Order 3 (quadratic) bspline curve
- An order 3 bspline curve has degree 2, i.e. is piecewise quadratic
- The curve does not pass through the control points (dark)
- There are (for uniform interior knots) span breaks (circles) at midpoints of interior edges.
- Span changes (circles) are exactly at the midpoints of polygon edges.
- Direction (slope, first derivative) is continuous at each span change (circles)
- The concavity (second derivative) changes abruptly at each span change (circles)
- This concavity change is not always visually obvious.
- These curves are not as smooth as your eye thinks.
- There are no concavity changes within any single span.
- Clamping (2 identical knots at start, 2 identical knots at end) makes the curve pass throught the end control points and point at neighbors.
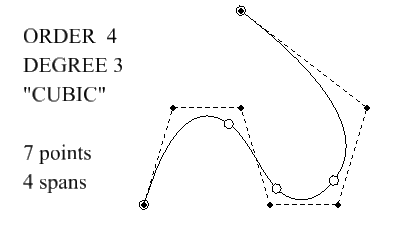
Example: Order 4 (cubic) bspline curve
- An order 4 bspline curve has degree 3, i.e. is piecewise cubic
- The curve does not pass through the control points (dark).
- The curve does not pass through particular points of the polygon edges.
- Span changes (circles) are generally "off the polygon"
- Direction and concavity are both continuous at span changes.
- There can be one concavity change within a span.
- Clamping (3 identical knots at start, 3 identical knots at end) makes the curve pass throught the end control points and point at neighbors.
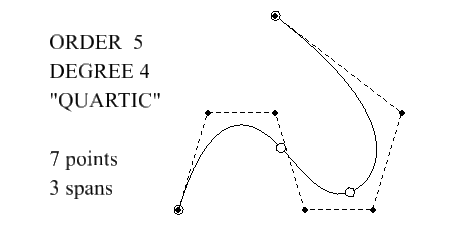
Example: Order 5 (quartic) bspline curve
- An order 5 bspline curve has degree 4, i.e. is piecewise quartic
- The curve does not pass through the control points (dark).
- The curve does not pass through particular points of the polygon edges.
- Span changes (circles) are generally "off the polygon"
- Direction, concavity, and one more derivative are all continuous at span changes.
- There can be two concavity change within a span.
- Clamping (4 identical knots at start, 4 identical knots at end) makes the curve pass throught the end control points and point at neighbors.
Last Updated: 08 January, 2020